Presented By-: Mohammad Rameez

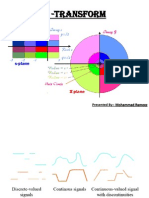
Types of Signals
Relation between various
transforms
5
Relation ship of Transformations
History

The z-transform was introduced, under this name,
by Ragazzini and Zadeh in 1952. The modified
or advanced Z-transform was later developed by E.
I. Jury, and presented in his bookSampled-Data
Control Systems (John Wiley & Sons 1958). The
idea contained within the Z-transform was
previously known as the "generating function
method."

Why z-Transform?
A generalization of Fourier transform
Why generalize it?
FT does not converge on all sequence
Notation good for analysis
Bring the power of complex variable theory deal with the
discrete-time signals and systems
In mathematics and signal processing, the Z-transform converts a discrete time-
domain signal, which is a sequence of real or complex numbers, into a
complex frequency-domain representation.
It can be considered as a discrete equivalent of the Laplace transform. This
similarity is explored in the theory of time scale calculus.
The z-transform is an extension of the discrete time. Fourier transform to a function
that is defined on regions of the complex plane. Some sequences that do not have
Fourier transforms will have z-transforms, but the reverse is true as well. For our
purposes, the special significance of z transform is as a tool to facilitate designing
systems with the desired attributes that can be practically implemented.

8
Definition of z-Transform
oThe z-transform of a discrete-time signal x(n) is
defined as the power series

(5.6)
where z is a complex variable.
oThis expression is two-sided z-transform.
oIf x(n) is a causal sequence, x(n) = 0 for n < 0,
then its z-transform is given by


oThis expression is one-sided z-transform.
( ) | | ( ) ( )

= =
n
n
z n x z X n x Z
( ) ( )

=
0 n
n
z n x z X
X(z) = E x[n] z
n

linear
difference
equation
time
domain
solution
z transformed
equation
z transform
solution
summing
algebra
z transform
inverse z transform
11
Introduction
oThe analysis of any sampled signal in frequency
domain is difficult using s-plane representation
(Laplace transform) because the equations will
contain infinite long polynomials due to the
characteristic infinite number of poles & zeroes.
oThis problem is overcome by z-transform, which
reduces the poles & zeroes to a finite number in
the z-plane.
oThe purpose of z-transform is to map any point s
= j in the s-plane to a corresponding point
z(r) in the z-plane by the relationship z = e
sT
.
14
+T is the sampling period. Hence,
z
-n
= e
-nsT

which correspond to a delay of n periods.
Therefore, the z-transform of x*(t) is given by:



oThe nth sample can be written as x(n) & thus


( ) | | ( ) ( )
n
n
z nT x z X t x Z

= =
0
*
( ) ( )
n
n
z n x z X

=
0
15
oEvaluating X(z) at the complex number z = re
j
:




oIf r = 1, the z-transform evaluated on the unit
circle gives the Fourier transform of the sequence
x(n)!
oz-transform is used to analyze discrete-time
systems for finding the transfer function, stability
& digital network realizations of the system.
( ) ( )( ) ( ) | |
n j
n
n
n
j
n
re z
e r n x re n x z X
j
e e
e

=
=

= =
z-Plane
Re
Im
z = e
je
e

=
n
n
z n x z X ) ( ) (
( ) ( )
j j n
n
X e x n e
e e

=
=

Fourier Transform is to evaluate z-transform
on a unit circle.
The z-transform is a function of the complex z variable
Convenient to describe on the complex z-plane
If we plot z=e
je
for e=0 to 2t we get the unit circle

z-plane
Re
Im
X(z)
Re
Im
z = e
je
e
Existence of the z Transform
Time Limited Signals
If a discrete-time signal x n
[ ]

is time limited and bounded,
the z transformation
summation x n
[ ]
z
- n

n=-

is
finite and the z transform of
x n
[ ]
exists for any non-zero
value of z.
20
Properties of Z Transform
Linearity
x
R z z X n x e = ), ( )] ( [ Z
y
R z z Y n y e = ), ( )] ( [ Z
y x
R R z z bY z aX n by n ax e + = + ), ( ) ( )] ( ) ( [ Z




Overlay of
the above two
ROCs
Shift
x
R z z X n x e = ), ( )] ( [ Z
x
n
R z z X z n n x e = + ) ( )] ( [
0
0
Z
Multiplication by an Exponential Sequence
+
< < =
x x-
R z R z X n x | | ), ( )] ( [ Z
x
n
R a z z a X n x a e =

| | ) ( )] ( [
1
Z
Differentiation of X(z)
x
R z z X n x e = ), ( )] ( [ Z
x
R z
dz
z dX
z n nx e =
) (
)] ( [ Z
Reversal
x
R z z X n x e = ), ( )] ( [ Z
x
R z z X n x / 1 ) ( )] ( [
1
e =

Z
Convolution of Sequences
x
R z z X n x e = ), ( )] ( [ Z
y
R z z Y n y e = ), ( )] ( [ Z
y x
R R z z Y z X n y n x e = ) ( ) ( )] ( * ) ( [ Z
28
Region of Convergence (ROC)
( ) <

n
n
r n x
Give a sequence, the set of values of z for
which the z-transform converges, i.e., |X(z)|<,
is called the region of convergence.
< = =


=

n
n
n
n
z n x z n x z X | || ) ( | ) ( | ) ( |
ROC is centered on origin and
consists of a set of rings.
Poles and Zeroes
) (
) (
) (
z Q
z P
z X =
where P(z) and Q(z) are
polynomials in z.
Zeros: The values of zs such that X(z) = 0
Poles: The values of zs such that X(z) =
30
oThe set of z values in the z-plane, for which the
magnitude of X(z) is finite is called the Region of
Convergence (ROC).
oThe condition for X(z) to be finite is |z| > 1 (area
outside the unit circle in the z-plane).
oThe ROC z-transform is bounded by the location
of its poles.
oExample, the z-transform of the unit step
response u(n) is given by

( )
1
=
z
z
z X
31
+which has a zero at z = 0 & a pole at z = 1.
+The ROC is |z| > 1 & extending all the way to .
32
Important Properties of ROC
(i) X(z) converges uniformly if & only if the ROC
of the z-transform X(z) includes the unit circle.
The ROC of X(z) consists of a ring in the z-
plane centered about the origin. The ROC of the
z-transform of x(n) has values of z for which
x(n)r
-n
is absolutely summable.


(ii)When x(n) is of finite duration, the ROC is the
entire z-plane, except possibly z = 0 & z = .
( ) <

n
n
r n x
33
(iii)If x(n) is a right-sided sequence, the ROC will
not include .

(iv)If x(n) is a left-sided sequence, the ROC will
not include z = 0. However, if x(n) = 0 for all
n > 0, the ROC will include z = 0.

(v)If x(n) is two-sided & if the circle |z| = r
o
is in
the ROC, the ROC will consist of a ring in the
z-plane that includes the circle |z| = r
o
.
34
(vi)If X(z) is rational, then the ROC extends to
infinity, i.e. the ROC is bounded by poles.

(vii)If x(n) is causal, the ROC includes z = .

(viii)If x(n) is anti-causal, the ROC includes z = 0.
35
36
37
Definition of Inverse
z-Transform
oThe inverse z-transform is derived to recover the
original time domain discrete signal x(n) from its
frequency domain signal X(z).

oThe operation can be expressed mathematically:

x(n) = Z
-1
[X(z)]
38
Evaluation of the Inverse
z-Transform
o There are basically three methods to perform
the inverse z-transform:

I) Long division method

II) Partial fraction expansion method

III)Residue method.
39
Long Division Method
oThe z-transform of a signal which is expressed
as the ratio of two polynomials in z, is simply
divided out to produce a power series in the form
of an equation.
oThe coefficients representing the sequence
values are in the time domain.



owhere the coefficients a
n
are the values of x(n).
( )
( )
( )

=

+ + + = = =
0
2
2
1
1
0
0
...
n
n
n
z a z a z a z a
z D
z N
z X
40
oThe coefficient of z
-K
is the Kth term in the
sequence.
oThe ROC will determine whether the series has
positive or negative exponents.
41
oFor right hand sequences (causal sequences) will
have primarily negative exponents, while left
hand sequences (anti-causal sequences) will have
positive exponents.

oFor annular ROC, a Laurent expansion will give
both the positive & negative exponents.
42
Partial Fraction Expansion Method
oIt is used to decompose a signal or a system
transfer function into a sum of standard functions.
oThe denominator of the transfer function H(z)
need to be factorized into prime factors.
oFor simple poles, H(z) can be expressed in the
following form with m s n,
( )
( )( ) ( )
n
m
m m m
o
p z p z p z
a z a z a z a
z H

+ + + +
=

...
...
2 1
2
2
1
1
( )
n
n
o
p z
A
p z
A
p z
A
A z H

+ +

+ = ...
2
2
1
1
43
+where




+With repeated linear roots, we have the terms:
( )
n m
n m
if
if a
z H
z
A
o
o
<
=

=

=
, 0
, lim
( ) ( ) . ,..., 3 , 2 , 1 n i for z H p z A
i
p z
i i
= =
=
( ) ( )
r
i
ir
i
i
i
i
p z
A
p z
A
p z
A

+ +

...
2
2 1
44
+where








+The inverse z-transform can be obtained from
the table.
( ) ( )
i
p z
r
i ir
z X p z A
=
=
( )
( ) ( )
i
p z
r
i r i
z X p z
dz
d
A
=

=
1
( )
( ) ( )
i
p z
r
i
k
k
k r i
z X p z
dz
d
k
A
=

=
!
1
( )
( ) ( )
i
p z
r
i
r
r
i
z X p z
dz
d
r
A
=

=
1
1
1
! 1
1
48
Property Signal z-transform
Transformation x(n)
Inverse transformation X(z)
Linearity a
1
x
1
(n) + a
2
x
2
(n) a
1
X
1
(z) + a
2
X
2
(z)
Time reversal x(-n) X(z
-1
)
Time shifting i) x(n - k)
ii) x(n + k)
i) z
-k
X(z)
ii) z
k
X(z)
Convolution x
1
(n) x
2
(n) X
1
(z)X
2
(z)
Correlation
Scaling a
n
x(n) X(a
-1
z)
Differentiation nx(n) or
Time differentiation x(n) - x(n - 1) X(z)(1 - z
-1
)
Time integration
Initial value theorem
Final value theorem
( ) ( )

=
0 n
n
z n x z X
( ) dz z z X
j
n 1
2
1

}
t
-
( ) ( ) ( )

=
=
n
x x
l n x n x l r
2 1
2 1 ( ) ( ) ( )
1
2 1
2 1

= z X z X z R
x x
( )
1
1

dz
z dX
z
( )
dz
z dX
z
( )

=0 k
k X
( ) n x
n 0
lim

( ) n x
n
lim
( )
|
.
|

\
|

=
1 z
z
z X
( ) z X
z
lim
( ) z X
z
z
z
|
.
|

\
|

1
1
lim
49
Signal x(t) Sequence
x[n]
z-Transform X(z) ROC
(t) [n] 1 All z-plane
(t - k) [n k] z
-k
|z| > 0, k > 0
|z| < , k < 0
u(t) u[n] |z| > 1
-u[-n 1] |z| < 1
r(t) = tu(t) nu[n] |z| > 1
a
n
u[n] |z| > |a|
-a
n
u[-n 1] |z| < |a|
1 1
1
1

z
z
z
1 1
1
1

z
z
z
( )
( )
2 2
1
1
1
1

=

z
z
z
z
a z
z
az
=

1
1
1
a z
z
az
=

1
1
1
z-Transform Pairs (1)
50
Signal x(t) Sequence
x[n]
z-Transform X(z) ROC
na
n
u[n] |z| > |a|
-na
n
u[-n 1] |z| < |a|
e
-at
e
an
|z| > |e
-a
|
t
2
n
2
u[n] |z| > 1
te
-at
ne
an
|z| > |e
-a
|
sin
o
t Sin
o
n |z| > 1
cos
o
t cos
o
n |z| > 1
( )
2
a z
az

( )
2
a z
az

a a
e z
z
z e

1
1
1
( )
( )
( )
( )
3 3
1
1
1
1
1
1
1

+
=

z
z z
z
z
z
( ) ( )
2 2
1
1
1
a
a
a
a
e z
ze
z e
e z

1 cos 2
sin
2
+
o
o
z z
z
e
e
( )
1 cos 2
cos
2
+

o
o
z z
z z
e
e
z-Transform Pairs (2)