Introduction to Computational Chemistry

NSF Computational Nanotechnology and Molecular Engineering

Pan-American Advanced Studies Institutes (PASI) Workshop
January 5-16, 2004
California Institute of Technology, Pasadena, CA
Andrew S. Ichimura
For the Beginner
There are three main problems:
1. Deciphering the language.
2. Technical implementation.
3. Quality assessment.
Focus on
Calculating molecular structures and relative
energies.
1. Hartree-Fock (Self-Consistent Field)
2. Electron Correlation
3. Basis sets and performance
Ab initio electronic structure theory
Hartree-Fock (HF)
Electron Correlation (MP2, CI, CC, etc.)
Molecular
properties
Geometry
prediction
Benchmarks for
parameterization
Transition States
Reaction coords.
Spectroscopic
observables
Prodding
Experimentalists
Goal: Insight into chemical phenomena.
Setting up the problem

What is a molecule?
A molecule is composed of atoms, or, more generally as a collection of charged
particles, positive nuclei and negative electrons.

The interaction between charged particles is described by;




Coulomb Potential

Coulomb interaction between these charged particles is the only important
physical force necessary to describe chemical phenomena.

V
ij
=V(r
ij
) =
q
i
q
j
4tc
0
r
ij
=
q
i
q
j
r
ij
r
ij
q
i
q
j
But, electrons and nuclei are in constant motion
In Classical Mechanics, the dynamics of a system (i.e. how the system
evolves in time) is described by Newtons 2nd Law:

F = ma
F = force
a = acceleration
r = position vector
m = particle mass

dV
dr
= m
d
2
r
dt
2
In Quantum Mechanics, particle behavior is described in terms of a wavefunction, +.


H += i
c+
ct
Hamiltonian Operator


H
Time-dependent Schrdinger Equation

i = 1; = h 2t
( )
Time-Independent Schrdinger Equation
If H is time-independent, the time-
dependence of + may be separated out as a
simple phase factor.


H (r,t) =

H (r)
+(r,t) = +(r)e
iEt /


H (r)+(r) = E+(r) Time-Independent Schrdinger Equation
Describes the particle-wave duality of electrons.
Hamiltonian for a system with N-particles
Sum of kinetic (T) and potential (V) energy


H =

T +

V


T =

T
i
=
2
2m
i i=1
N

i=1
N

V
i
2
=
2
2m
i i=1
N

c
2
cx
i
2
+
c
2
cy
i
2
+
c
2
cz
i
2
|
\

|
.
|

V
i
2
=
c
2
cx
i
2
+
c
2
cy
i
2
+
c
2
cz
i
2
|
\

|
.
|
Laplacian operator
Kinetic energy


V = V
ij
j>1
N

i=1
N

=
q
i
q
j
r
ij j>1
N

i=1
N

Potential energy
When these expressions are used in the time-independent Schrodinger Equation,
the dynamics of all electrons and nuclei in a molecule or atom are taken into
account.
Born-Oppenheimer Approximation
Since nuclei are much heavier than electrons, their velocities are much
smaller. To a good approximation, the Schrdinger equation can be
separated into two parts:
One part describes the electronic wavefunction for a fixed nuclear
geometry.
The second describes the nuclear wavefunction, where the electronic
energy plays the role of a potential energy.


So far, the Hamiltonian contains the following terms:


H =

T
n
+

T
e
+

V
ne
+
+

V
ee
+

V
nn


T
n
Kinetic energy of nuclei, n


T
e
Kinetic energy of electrons, e


V
ne
Electron-nuclear attraction


V
ee
Electron-electron repulsion


V
nn
Internuclear repulsion
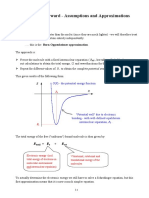
Born-Oppenheimer Approx. cont.
In other words, the kinetic energy of the nuclei can be treated separately. This
is the Born-Oppenheimer approximation. As a result, the electronic
wavefunction depends only on the positions of the nuclei.

Physically, this implies that the nuclei move on a potential energy surface
(PES), which are solutions to the electronic Schrdinger equation. Under the
BO approx., the PES is independent of the nuclear masses; that is, it is the
same for isotopic molecules.






Solution of the nuclear wavefunction leads to physically meaningful
quantities such as molecular vibrations and rotations.
0
E
H H
H
.
+ H
.
Limitations of the Born-Oppenheimer approximation
The total wavefunction is limited to one electronic surface, i.e. a particular
electronic state.
The BO approx. is usually very good, but breaks down when two (or more)
electronic states are close in energy at particular nuclear geometries. In such
situations, a non-adiabatic wavefunction - a product of nuclear and
electronic wavefunctions - must be used.
In writing the Hamiltonian as a sum of electron kinetic and potential energy
terms, relativistic effects have been ignored. These are normally negligible
for lighter elements (Z<36), but not for the 4
th
period or higher.
By neglecting relativistic effects, electron spin must be introduced in an ad
hoc fashion. Spin-dependent terms, e.g., spin-orbit or spin-spin coupling may
be calculated as corrections after the electronic Schrdinger equation has
been solved.
The electronic Hamiltonian becomes,


H =

T
e
+

V
ne+
+

V
ee
+

V
nn
B.O. approx.; fixed nuclear coord.
Self-consistent Field (SCF) Theory
GOAL: Solve the electronic Schrdinger equation, H
e
+=E+.

PROBLEM: Exact solutions can only be found for one-electron systems,
e.g., H
2
+
.

SOLUTION: Use the variational principle to generate approximate
solutions.
Variational principle - If an approximate wavefunction is used in
H
e
+=E+, then the energy must be greater than or equal to the exact
energy. The equality holds when + is the exact wavefunction.
In practice: Generate the best trial function that has a number of
adjustable parameters. The energy is minimized as a function of these
parameters.

SCF cont.
The energy is calculated as an expectation value of the Hamiltonian operator:




E =
+
-
}

H
e
+dt
+
-
+dt
}
Introduce bra-ket notation,

+
-
}

H
e
+dt = +|

H
e
| +

+
-
+dt
}
= +| +
bra

n
complex conjugate , left
ket

m
right
Combined bracket denotes integration over all coordinates.

E =
+ |

H
e
| +
+| +
If the wavefunctions are orthogonal and normalized (orthonormal),

+
i
| +
j
=o
ij

o
ij
= 1
o
ij
= 0
Then,

E = +|

H
e
| +
(Kroenecker delta)
SCF cont.
Antisymmetric wavefunctions can be written as
Slater determinants.
Since electrons are fermions, S=1/2, the total electronic wavefunction must be
antisymmetric (change sign) with respect to the interchange of any two electron
coordinates. (Pauli principle - no two electrons can have the same set of quantum
numbers.)
Consider a two electron system, e.g. He or H
2
. A suitable antisymmetric
wavefunction to describe the ground state is:

u1,2 ( ) =|
1
o(1)|
2
|(2) |
1
o(2)|
2
|(1)
Each electron resides in a spin-orbital, a product of spatial and spin functions.

(Spin functions are orthonormal: o | o = | | | =1; o | | = | | o = 0)

u 2,1 ( ) = |
1
o(2)|
2
|(1) |
1
o(1)|
2
|(2)
u 2,1 ( ) = u 1, 2 ( )
Interchange the coordinates of the two electrons,
(He: |
1
=|
2
= 1s)
(H
2
: |
1
= |
2
= |
bonding MO
)
A more general way to represent antisymmetric electronic wavefunctions is in the
form of a determinant. For the two-electron case,

u 1,2 ( ) =
|
1
o(1) |
2
|(1)
|
1
o(2) |
2
|(2)
= |
1
o(1)|
2
|(2) |
1
o(2)|
2
|(1)
For an N-electron N-spinorbital wavefunction,

u
SD
=
|
1
1 ( ) |
2
(1) |
N
(1)
|
1
2 ( ) |
2
(2) |
N
(2)
|
1
N ( ) |
2
(N) |
N
(N)
, |
i
||
j
= o
ij
A Slater Determinant (SD) satisfies the antisymmetry requirement.
Columns are one-electron wavefunctions, molecular orbitals.
Rows contain the electron coordinates.
One more approximation: The trial wavefunction will consist of a single SD.
Now the variational principle is used to derive the Hartree-Fock equations...
SCF cont.
Hartree-Fock Equations
(1) Reformulate the Slater Determinant as,

u =

A |
1
(1)|
2
(2) |
N
(N)
| |
=

A H

H is the diagonal product


A the antisymmetrizer


A =
1
N!
(1)
p

P
p =0
N1

=
1
N!
1

P
ij
+

P
ijk

ijk

ij

(

(
(


P is the permutation operator.

P
ij
permutes two electron coordinates.
(2)


H
e
=

T
e
+

V
ne+
+

V
ee
+

V
nn


T
e
=
1
2
V
i
2
i
N

V
ne
=
Z
a
R
a
r
i a

i
N

V
ee
=
1
r
i
r
j
j >i
N

i
N

V
nn
=
Z
a
Z
b
R
a
R
b b >a

One electron
terms

}
Depends on
two electrons


h
i
=
1
2
V
i
2

Z
a
R
a
r
i
a

g
ij
=
1
r
i
r
j

H
e
=

h
i
i =1
N

+

g
ij
j >i
N

i
N

+

V
nn
One-electron operator - describes electron
i, moving in the field of the nuclei.
Two-electron operator - interelectron
repulsion.
Hamiltonian
Expectation value over
Slater Determinant

E
e
= u|

H
e
| u
E
e
=

A H|

H
e
|

A H = (1)
p
p=0
N1

H|

H
e
|

P H
(3) Calculation of the energy.
Examine specific integrals:

u|

V
nn
| u =V
nn
Nuclear repulsion does not depend
on electron coordinates.
The one-electron operator acts only on electron 1 and yields
an energy, h
1
, that depends only on the kinetic energy and
attraction to all nuclei.
For coordinate 1,

H|

h
1
| H = |
1
(1)|
2
(2) |
N
(N)
| |
|

h
1
| |
1
(1)|
2
(2) |
N
(N)
| |
= |
1
(1) |

h
1
| |
1
(1) |
2
(2) ||
2
(2) |
N
(N) | |
N
(N) = h
1

H|

g
12
| H = |
1
(1)|
2
(2) |
N
(N)
| |
|

g
12
| |
1
(1)|
2
(2) |
N
(N)
| |
= |
1
(1)|
2
(2) |

g
12
| |
1
(1)|
2
(2) |
3
(3) ||
3
(3) |
N
(N) | |
N
(N)
= |
1
(1)|
2
(2) |

g
12
| |
1
(1)|
2
(2) = J
12
Coulomb integral, J
12
: represents the classical repulsion
between two charge distributions |
1
2
(1) and |
2
2
(2).

H|

g
12
|

P
12
H = |
1
(1)|
2
(2) |
N
(N)
| |
|

g
12
| |
2
(1)|
1
(2) |
N
(N)
| |
= |
1
(1)|
2
(2) |

g
12
| |
2
(1)|
1
(2) |
3
(3) ||
3
(3) |
N
(N) | |
N
(N)
= |
1
(1)|
2
(2) |

g
12
| |
2
(1)|
1
(2) = K
12
Exchange integral, K
12
: no classical analogue. Responsible for
chemical bonds.
The expression for the energy can now be written as:
Sum of one-electron, Coulomb,
and exchange integrals, and V
nn
.
To apply the variational principle, the Coulomb and Exchange integrals are
written as operators,

E
e
= |
i
|

h
i
| |
i
i =1
N

+
1
2
|
j
|

J
i
||
j
|
j
|

K
i
||
j
( )
j
N

i
N

+ V
nn


J
i
||
j
(2) = |
i
(1) |

g
12
| |
i
(1) |
j
(2)


K
i
||
j
(2) = |
i
(1) |

g
12
| |
j
(1) |
i
(2)

E
e
= h
i
i =1
N

+
1
2
(J
ij
K
ij
)
j
N

i
N

+ V
nn
The objective now is to find the best orbitals (|
i
, MOs) that minimize the
energy (or at least remain stationary with respect to further changes in |
i
),
while maintaining orthonormality of |
i
.
Employ the method of Langrange Multipliers:

f (x
1
, x
2
, x
N
)
g(x
1
, x
2
, x
N
) = 0
L(x
1
, x
2
, x
N
,) = f (x
1
, x
2
, x
N
) g(x
1
, x
2
, x
N
)
Optimize L such that
cL
cx
i
= 0,
cL
c
i
= 0
Function to optimize.
Rewrite in terms of another function.
Define Lagrange
function.
Constrained optimization of L.

L = E
ij
|
i
| |
j
o
ij
( )
ij
N

oL = oE
ij
o|
i
| |
j
+ |
i
|o|
j
( )
ij
N

= 0
In terms of molecular orbitals, the Langrange function is:
Change in L with respect to small
changes in |
i
should be zero.

oE = o|
i
|

h
i
||
i
+ |
i
|

h
i
| o|
i
( )
i =1
N

+ o|
i
|

J
j


K
j
| |
i
+ |
i
|

J
j


K
j
| o|
i
( )
ij
N

Change in the energy with respect changes in |

i
.
Define the Fock Operator, F
i



F
i
=

h
i
+

J
j


K
j
( )
j
N

Effective one-electron operator, associated

with the variation in the energy.

oE = o|
i
|

F
i
| |
i
+ |
i
|

F
i
| o|
i
( )
i =1
N

Change in energy in terms

of the Fock operator.

oL = o|
i
|

F
i
||
i
+ |
i
|

F
i
|o|
i
( )
i=1
N

ij
o|
i
| |
j
+ |
i
|o|
j
( )
ij
N

= 0
According to the variational principle, the best orbitals, |
i
, will make oL=0.


F
i
|
i
=
ij
|
j
j
N

After some algebra, the final expression becomes:

Hartree-Fock Equations
After a unitary transformation,
ij
0 and
ii
c
i
.


F
i
|
i
' = c
i
|
i
'
HF equations in terms of Canonical MOs and
diagonal Lagrange multipliers.

c
i
= |
i
' |

F
i
||
i
'
Lagrange multipliers can be interpreted as
MO energies.
Note:
1. The HF equations cast in this way, form a set of pseudo-eigenvalue
equations.
2. A specific Fock orbital can only be determined once all the other
occupied orbitals are known.
3. The HF equations are solved iteratively. Guess, calculate the
energy, improve the guess, recalculate, etc.
4. A set of orbitals that is a solution to the HF equations are called
Self-consistent Field (SCF) orbitals.
5. The Canonical MOs are a convenient set of functions to use in the
variational procedure, but they are not unique from the standpoint
of calculating the energy.
Koopmans Theorem
The ionization energy is well approximated by the orbital energy, c
i
.
* Calculated according to Koopmans theorem.
Basis Set Approximation
For atoms and diatomic molecules, numerical HF methods are available.
In most molecular calculations, the unknown MOs are expressed in terms of a
known set of functions - a basis set.

Two criteria for selecting basis functions.
I) They should be physically meaningful.
ii) computation of the integrals should be tractable.

It is common practice to use a linear expansion of Gaussian functions in the MO
basis because they are easy to handle computationally.






Each MO is expanded in a set of basis functions centered at the nuclei and are
commonly called Atomic Orbitals.
(Molecular orbital = Linear Combination of Atomic Orbitals - LCAO).
MO Expansion

|
i
= c
oi
_
o
o
M

F
i
c
oi
_
o
o
M

= c
i
c
oi
_
o
o
M

FC= SCc
F
o|
= _
o
|

F | _
|
S
o|
= _
o
| _
|
LCAO - MO representation
Coefficients are variational parameters
HF equations in the AO basis
Matrix representation of HF eqns.
Roothaan-Hall equations (closed shell)
F
o|
- element of the Fock matrix
S
o|
- overlap of two AOs
Roothaan-Hall equations generate M molecular orbitals from M basis functions.
N-occupied MOs
M-N virtual or unoccupied MOs (no physical interpretation)
Total Energy in MO basis
One-electron integrals, M
2
Two-electron integrals, M
4
Computed at the start; do not change
Products of AO coeff form Density Matrix, D

E = |
i
|

h
i
| |
i
i =1
N

+
1
2
|
i
|
j
|

g ||
i
|
j
|
i
|
j
|

g | |
j
|
i
( )
j
N

i
N

+V
nn

E = c
oi
c
|i
o|
M

_
o
|

h
i
| _
|
i =1
N

+
1
2
c
oi
c
j
c
|i
c
oj
_
o
_

|

g | _
|
_
o
_
o
_

|

g | _
o
_
|
( )
+ V
nn
o|o
M

ij
N

Total Energy in AO basis

D
o
= c
j
c
oj
j
occ.MO

; D
o|
= c
oi
c
|i
i
occ.MO

General SCF Procedure

Obtain initial guess
for coeff., c
oi
,form
the initial D
o

Form the Fock matrix
Diagonalize the Fock Matrix
Form new Density Matrix
Two-electron
integrals
Iterate
Computational Effort
Accuracy
As the number of functions increases, the accuracy of the Molecular Orbitals
improves.
As M, the complete basis set limit is reached Hartree-Fock limit.

Result: The best single determinant wavefunction that can be obtained.
(This is not the exact solution to the Schrodinger equation.)

Practical Limitation
In practice, a finite basis set is used; the HF limit is never reached.
The term Hartree-Fock is often used to describe SCF calculations with
incomplete basis sets.
Formally, the SCF procedure scales as M
4
(the number of basis
functions to the 4th power).
Restricted and Unrestricted Hartree-Fock
1
2
3
4
5
RHF
Singlet
ROHF
Doublet
UHF
Doublet
o |
Energy
Restricted Hartree-Fock (RHF)
For even electron, closed-shell singlet states, electrons in a given MO
with o and | spin are constrained to have the same spatial dependence.
Restricted Open-shell Hartree-Fock (ROHF)
The spatial part of the doubly occupied orbitals are restricted to be the same.
Unrestricted Hartree-fock (UHF)
o and | spinorbitals have different spatial parts.

}
Spinorbitals
|
i
o(n)
Comparison of RHF and UHF
R(O)HF
o and | spins have same spatial
part

Wavefunction, u, is an
eigenfunction of S
2
operator.

For open-shell systems, the
unpaired electron (o) interacts
differently with o and | spins.
The optimum spatial orbitals are
different. Restricted
formalism is not suitable for spin
dependent properties.

Starting point for more advanced
calculations that include electron
correlation.
UHF
o and | spins have different
spatial parts

Wavefunction is not an
eigenfunction of S
2
. u may be
contaminated with states of
higher multiplicity (2S+1).

E
UHF
E
R(O)HF


Yields qualitatively correct
spin densities.

Starting point for more
advanced calculations that
include electron correlation.
Ab Initio (latin, from the beginning) Quantum Chemistry
Summary of approximations
Born-Oppenheimer Approx.
Non-relativistic Hamiltonian
Use of trial functions, MOs, in the variational procedure
Single Slater determinant
Basis set, LCAO-MO approx.
RHF, ROHF, UHF
Consequence of using a single Slater determinant and
the Self-consistent Field equations:
Electron-electron repulsion is included as an average effect. The electron
repulsion felt by one electron is an average potential field of all the others,
assuming that their spatial distribution is represented by orbitals. This is
sometimes referred to as the Mean Field Approximation.
Electron correlation has been neglected!!!