Professional Documents
Culture Documents
CHP 5
CHP 5
Uploaded by
AnindyaSahaOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
CHP 5
CHP 5
Uploaded by
AnindyaSahaCopyright:
Available Formats
5.
1 the frequency response of LTI system
5.2 system function
5.3 frequency response for rational system function
5.4 relationship between magnitude and phase
5.5 all-pass system
5.6 minimum-phase system
5.7 linear system with generalized linear phase
Chapter 5 transform analysis of linear
time-invariant system
5.1 the frequency response of LTI system
) (
| ) ( | ) (
] [ ) (
e
e e
e e
j
e H j j j
n
n j j
e e H e H
e n h e H
Z
=
=
| ) ( | . 1
e j
e H
magnitude response or gain
) ( ) ( | ) ( | . 2
2 e e e j j j
e H e H e H
-
=
magnitude square function
dB unit e H
j
: |, ) ( | log 20 . 3
10
e
log magnitude
| ) ( | log 20
10
e j
e H
magnitude attenuation
magnitude-frequency characteristic
log magnitude
linear magnitude
transform curve
from linear to log
magnitude
phase-frequency characteristic
) ( . 4
e j
e H Z
phase response
t t
e
s < )] ( [ . 5
j
e H ARG
principal phase
)] ( arg[ . 6
e j
e H
continuous phase
e
e
e
d
e H d
e H grd
j
j
)] ( arg[
)] ( [ . 7 =
group delay
Figure 5.7
Figure 5.1 EXAMPLE
understand group delay
Figure 5.2
t t t e 5 . 0 , 25 . 0 , 85 . 0 =
t t e 25 . 0 , 5 . 0 =
5.2 system function
=
n
n
z n h z H ] [ ) (
Characteristics of zeros and poles
1take origin and zeros and poles at infinite into consideration, the numbers of
zeros and poles are the same.
2for real coefficient, complex zeros and poles are conjugated, respectively.
3if causal and stable, poles are all in the unit circle.
4FIRhave no nonzero poles, called all-zeros type, steady
IIRhave nonzero pole; if no nonzero zeros , called all-poles type
] 1 [ ] [ ] [
1
1
1
) (
] 1 [ ] 1 [ ] [ ] [
1
1
2
+ =
+ =
=
+ =
n x n x n y
z
z
z
z H
n y n x n x n y
EXAMPLE
Difference about
zeros and poles in
FIR and IIR
) ( ) (
e j
e H z H
5.3 frequency response for rational system function
e
e
j
e z
j
z H e H
=
= | ) ( ) (
1.formular method
2. Geometrical method
[
[
=
=
=
N
k
k
M
k
k
M N
d z
c z
Bz z H
1
1
) (
) (
) (
e
e e e
e
e
e
e
) ( | ] arg[ ] arg[ ] arg[ )] ( arg[
| |
| |
| | | ) ( | | ) ( |
1 1
1
1
M N d e c e B e H
d e
c e
B z H e H
N
k
k
j
M
k
k
j j
N
k
k
j
M
k
k
j
e z
j
j
+ + =
= =
[
[
= =
=
=
=
3 2 1
3 2
1
)] ( arg[ , | | | ) ( | u u u + = = e
e e j j
e H
L L
L
B e H
EXAMPLE
magnitude response in w near zeros is minimum, there are zeros in unit circle, then
the magnitude is 0
magnitude response in w near poles is maximumzeros and poles counteracted each
other and in origin does not influence the magnitude.
| ) ( |
e j
e H
) 1 /( 1 a
) 1 /( 1 a +
t t 2 0
| | | | ,
1
1
) (
1
a z
az
z H >
=
EXAMPLE
t t 2 0
)] ( arg{
e j
e H
a
] 4 [ ] [ ] [ = n x n x n y
EXAMPLE
B=1
A=[1,-0.5]
figure(1)
zplane(B,A)
figure(2)
freqz(B,A)
figure(3)
grpdelay(B,A,10)
1
5 . 0 1
1
) (
=
z
z H
EXAMPLE
3.matlab method
5.4 relationship between magnitude and phase
) ( | ) ( | z H e H
j
e
poles reciprocal conjugate 4
zeros reciprocal conjugate 4
) ( | ) ( | ) / 1 ( ) ( | ) ( |
nonuniform
2 * *
uniform
2
|
= = z H e H z H z H e H z e
j j
je
e e
Figure 5.20
6 5 4
3 5 4
6 2 1
3 2 1
3 2 1
, ,
, ,
, ,
, ,
, ,
z z z
z z z
z z z
z z z
p p p
EXAMPLE
) / 1 ( ) (
* *
z H z H
Pole-zero plot for H(z): causal and stable
Confirm the poles and zeros
5.5 all-pass system
t cons e H
j
ap
tan | ) ( | =
e
[ [
=
|
|
.
|
\
|
=
c r
M
k
k
k
k
k
M
k
k
k
ap
z e
e z
z e
e z
z d
d z
A z H
1
1 *
1
1
* 1
1
1
1
) 1 (
) (
) 1 (
) (
1
) (
Zeros and poles are conjugate reciprocal
For real coefficient, zeros are conjugated , poles are conjugated.
4/3
3/4
EXAMPLE
Y
Y
Y
N
0 )] ( [ >
e j
ap
e H grd
t e
e
< < < 0 , 0 )] ( arg[ for e H
j
ap
Characteristics of causal and stable all-pass system:
| ) ( ' | | ) ( | ), ( ' ) ( ) (
e e j j
ap
e H e H z H z H z H = =
application
1. compensate the phase distortion
2. compensate the magnitude distortion together with minimum-phase system
) ( ) ( ). (
min
z H z H z H
ap
=
5.6 minimum-phase system
] [ ] [ * ] [ * ] [ ,
], [ ] [ * ] [ :
) ( ) ( ) ( ) ( ,
) ( / 1 ) ( , , 1 ) ( ) (
n x n h n h n x then
n n h n h or
z X z H z H z X then
z H z H is that z H z H
i
i
i
i i
=
=
=
= =
o
inverse system:
on intersecti have must ) ( and ) ( of
:, ] [ ] [ * ] [ of condition the
z H z H ROC
n n h n h
i
i
o =
explanation
1not all the systems have inverse system
2inverse system may be nonuniform
3the inverse system of causal and stable system may not be causal and stable
the condition of both original and its inverse system causal and stable
zeros and poles are all in the unit circlesuch system is called minimum-
phase system,
corresponding h[n] is minimum-phase sequence
poles are all in the unit circle, zeros are all outside the unit circle, such
system is called maximum-phase system
| ) ( | | ) ( |
) ( ) ( ) (
min
min
e e j j
ap
e H e H
z H z H z H
=
=
zeros outside the
unit circle
poles outside
the unit circle
minimum-phase system:
conjugate reciprocal
zeros and poles
all-pass system: counteracted
zeros and poles, zeros and
poles outside the circle
minimum-phase and all-pass decomposition
If H(z) is rational, then :
) ( ) ( ) ( ) ( :
,
) (
1
) ( ), ( ) ( ) (
min
min
z H z H z H z H system total
z H
z H z H z H z H
ap c d
c ap d
= =
= =
Figure 5.25
Application of minimum-phase and all-pass decomposition
Compensate for amplitude distortion
Properties of minimum-phase systems:
) ( ) ( ) (
min
z H z H z H
ap
=
| ) ( | | ) ( |
min
e e j j
e H e H =
1minimum phase-delay
t e
e
e e
s s <
<
0 , 0 )] ( arg[
)] ( arg[ )] ( arg[
min
j
ap
j j
e H
e H e H
2minimum group-delay
0 )] ( [
)] ( [ )] ( [
min
>
<
e
e e
j
ap
j j
e H grd
e H grd e H grd
Minimum-phase system and some all-pass system in cascade can make up of another
system having the same magnitude response, so there are infinite systems having the
same magnitude response.
< >
=
=
=
>
=
=
=
n n E n E but
E E then
n h n h
e H e H
n E n E
then m h n E define
n n
j j
n
m
], [ ] [ ,
] [ ] [ ,
| ] [ | | ] [ |
| ) ( | | ) ( |
] [ ] [
, energy partial | ] [ | ] [ :
min
min
0
2
min
0
2
min
min
0
2
e e
3minimum energy-delayi.e. the partial energy is most concentrated around n=0
Figure 5.30
maximum phase
EXAMPLE
minimum phase
Systems having the same
magnitude response
Figure 5.31
minimum phase
Figure 5.32
5.7 linear system with generalized linear phase
5.7.1 definition
5.7.2 conditions of generalized linear phase system
5.7.3 causal generalized linear phase (FIR)system
5.7.1 definition
) ( )] ( [ ), ( )] ( arg[
| | | ) ( | ) (
real e H grd line e H
e e H e H
j j
j j j
o eo
t e
e e
eo e e
= =
< =
Strict:
o
| eo
t e
e
e
e
| eo e e
=
+ =
< =
+
)] ( [
, )] ( arg[
) (
| | ) ( ) (
j
j
j
j j j j
e H grd
e H
function real a is e A
e e A e H
Generalized:
Systems having constant group delay
phase
t e
o
e e
< =
= - =
=
| | ) (
] [ ] [ ] [ ] [
] [ ] [
m j j
id
id
id
e e H
m n x n h n x n y
m n n h
EXAMPLE
ideal delay system
T
e A e
T
T j e H
j j j
e
t | o
e
e
e t e
= = = = = ) ( , 2 / , 0 , / ) (
2 /
differentiatormagnitude and phase are all linear
EXAMPLE
physical meaning
all components of input signal are delayed by the same amount in strict
linear phase system then there is only magnitude distortion, no phase distortion.
it is very important for image signal and high-fidelity audio signal to have no
phase distortion.
when B=0, for generalized linear phase, the phase in the whole band is not
linear, but is linear in the pass band, because the phase +PI only occurs when
magnitude is 0, and the magnitude in the pass band is not 0.
square wave with fundamental
frequency 100 Hz
linear phase filter
lowpass filter with cut-off
frequency 400Hz
nonlinear phase filter
lowpass filter with cut-off
frequency 400Hz
EXAMPLE
Generalized linear phase in the
pass band is strict linear phase
Generalized linear phase in the
pass band is strict linear phase
5.7.2 conditions of generalized linear phase system
=
=
=
=
=
=
] [ ] 2 [
) (int 2
2 / 3 2 /
) 2 (
] [ ] 2 [
) (int 2
0
) 1 (
n h n h
eger M
or
n h n h
eger M
or
o
o
t t |
o
o
t |
=
=
= =
=
=
= =
2 /
2 / 3 2 /
: , int
, ,... ], [ ] [ : ) 2 (
2 /
0
: , int
, ,... ], [ ] [ : ) 1 (
M
or
then eger a is M
n n h n M h if
M
or
then eger a is M
n n h n M h if
o
t t |
o
t |
Or:
Figure 5.35
M:even
M:odd
M:not integer
EXAMPLE
M:not integer
determine whether these system is linear phase,generalized or strict?a and =?
2
2
3
1
2
1
3
EXAMPLE
(1) (2)
(3)
(4)
5.7.3 causal generalized linear phase (FIR)system
M n or n for n h
M n n M h n h
> < =
s s =
0 , 0 ] [
0 ], [ ] [
odd M n M h n h
typeIV
even M n M h n h
typeIII
odd M n M h n h
typeII
even M n M h n h
typeI
: ], [ ] [
: ) 4 (
: ], [ ] [
: ) 3 (
: ], [ ] [
: ) 2 (
: ], [ ] [
: ) 1 (
=
=
=
=
Magnitude and phase characteristics of the 4 types
2 /
2
) ( t e e + = u
M
=
(
|
.
|
\
|
=
M
n
j
n
M
n h e A
0
2 2
cos ) ( ) (
t
e
e
2 / ... 2 , 1 ], 2 / [ 2 ] [ ], 2 / [ ] 0 [ :
) cos( ] [
2
cos ] [ ) ( :
2 /
0 0
M k k M h k a M h a where
k k a n
M
n h e A typeI
M
k
M
n
j
= = =
=
(
|
.
|
\
|
=
= =
e e
e
2 / ) 1 ...( 2 , 1 ], 2 / ) 1 [( 2 ] [ :
)) 2 / 1 ( cos( ] [
2
cos ] [ ) ( :
2 /
0 0
+ = + =
=
(
|
.
|
\
|
=
= =
M k k M h k b where
k k b n
M
n h e A typeII
M
k
M
n
j
e e
e
2 / ... 2 , 1 ], 2 / [ 2 ] [ :
) sin( ] [
2
cos ] [ ) ( :
2 /
0 0
M k k M h k c where
k k c n
M
n h e A typeIII
M
k
M
n
j
= =
=
(
|
.
|
\
|
=
= =
e e
e
2 / ) 1 ...( 2 , 1 ], 2 / ) 1 [( 2 ] [ :
)) 2 / 1 ( sin( ] [
2
cos ] [ ) ( :
2 /
0 0
+ = + =
=
(
|
.
|
\
|
=
= =
M k k M h k d where
k k d n
M
n h e A typeIV
M
k
M
n
j
e e
e
| ) ( |
e j
e H
I II
)} ( {
e j
e H ARG
)} ( {
e j
e H grd
III IV
| ) ( |
e j
e H
)} ( {
e j
e H ARG
)} ( {
e j
e H grd
z5
z4
z3*
z3
1/z2
1/z
1
*
1/z1
z1
z1*
z2
Characteristic of zeros: commonness
Figure 5.41
Characteristic of every type
0 ) ( =
t j
e H
type I
type II
type III
type IV
0 ) ( , 0 ) (
0
= =
t j j
e H e H
0 ) (
0
=
j
e H
characteristic of magnitude get from characteristic of zeros
M is even M is odd
low high band pass band stop low high band pass band stop
h[n] is even (I) Y Y Y Y Y N Y N (II)
h[n] is odd (III) N N Y N N Y Y N (IV)
Application of 4 types of linear phase system:
5.1 the frequency response of LTI system :
5.2 system function
5.3 frequency response for rational system function:
5.4 relationship between magnitude and phase :
5.5 all-pass system
5.6 minimum-phase system
5.7 linear system with generalized linear phase FIR)
5.7.1 definition:
5.7.2 conditions : h[n] is symmetrical
5.7.3 causal generalized linear phase system
1.condition
2.classification
3.characteristics of magnitude and phase , filters in point respectively
4.analyse of characteristic of magnitude from the zeros of system function
) (
e j
e H
) ( ) (
e j
e H z H
) ( | ) ( |
2
z H e H
j
e
t e
eo e e
< =
| | ) ( ) (
j j j
e e A e H
summary
requirement:
concept of magnitude and phase response, group delay;
transformation among system function, phase response and
difference equation;
concept of all-pass, minimum-phase and linear phase system and
characteristic of zeros and poles;
minimum-phase and all-pass decomposition;
conditions of linear phase system , restriction of using as filters
key and difficulty
linear phase system
exercises
5.17 complementarityminimum-phase and all-pass decomposition
5.21
5.45
5.53
the first experiment
problem 1D
problem 11
problem 13C
problem 22A
problem 24AC
Get subjects from the experiment instruction book or downloading from network
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5822)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1093)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (852)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (898)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (349)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (403)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Cache Dirt 5700Document5 pagesCache Dirt 5700David LynxNo ratings yet
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Geospatial JeopardyDocument54 pagesGeospatial JeopardyrunnealsNo ratings yet
- AMCA Series Multilayer Chip Antenna Application NoteDocument16 pagesAMCA Series Multilayer Chip Antenna Application NoteAnindyaSahaNo ratings yet
- Aurasemi - RF BU - Introduction - Team & RoadmapDocument25 pagesAurasemi - RF BU - Introduction - Team & RoadmapAnindyaSahaNo ratings yet
- Tunable NPath NotchFilter ForBlockerSuppression 11489294Document31 pagesTunable NPath NotchFilter ForBlockerSuppression 11489294AnindyaSahaNo ratings yet
- AU5508 Servo Solution PresentationDocument9 pagesAU5508 Servo Solution PresentationAnindyaSaha100% (1)
- Aurasemi LDO Products IntroductionDocument19 pagesAurasemi LDO Products IntroductionAnindyaSahaNo ratings yet
- Currisc PDFDocument10 pagesCurrisc PDFAnindyaSahaNo ratings yet
- Altaf ShaikDocument11 pagesAltaf ShaikAnindyaSahaNo ratings yet
- Who and How Making 5g NR StandardsDocument16 pagesWho and How Making 5g NR StandardsAnindyaSahaNo ratings yet
- LoRaWAN Specification 1R0Document82 pagesLoRaWAN Specification 1R0AnindyaSahaNo ratings yet
- OverDocument21 pagesOverAnindyaSahaNo ratings yet
- Time Domain Equalizers - V3Document15 pagesTime Domain Equalizers - V3AnindyaSahaNo ratings yet
- 48V TXT Service Manual PDFDocument192 pages48V TXT Service Manual PDFJim Campbell De Castro100% (3)
- Module One Wellness PlanDocument10 pagesModule One Wellness PlanMatthew JohnsonNo ratings yet
- CatapultDocument4 pagesCatapultapi-305320178No ratings yet
- Catalog GIPPS (March 2023) - EnglishDocument16 pagesCatalog GIPPS (March 2023) - EnglishgbcomsrlNo ratings yet
- Term-2 - Grade 8 Social Science Mock Test-2Document4 pagesTerm-2 - Grade 8 Social Science Mock Test-2bhagatNo ratings yet
- Problem 2.32 PDFDocument1 pageProblem 2.32 PDFKauê BrittoNo ratings yet
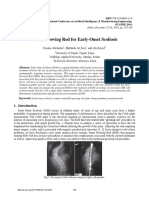
- Smart Growing Rod For Early-Onset Scoliosis: Osama Abolaeha, Huthaifa Al - Issa, and Ali ZayedDocument7 pagesSmart Growing Rod For Early-Onset Scoliosis: Osama Abolaeha, Huthaifa Al - Issa, and Ali ZayedfajarvicNo ratings yet
- Seminar Nasional - VII Rekayasa Dan Aplikasi Teknik Mesin Di IndustriDocument4 pagesSeminar Nasional - VII Rekayasa Dan Aplikasi Teknik Mesin Di IndustrizaenalNo ratings yet
- NURS FPX 6214 Assessment 4 Staff Training SessionDocument6 pagesNURS FPX 6214 Assessment 4 Staff Training SessionCarolyn HarkerNo ratings yet
- Emaco Nanocrete R3 - PDS - ASEAN - 241110Document3 pagesEmaco Nanocrete R3 - PDS - ASEAN - 241110Andri AjaNo ratings yet
- Bim Brochure Us May 2019 PDFDocument20 pagesBim Brochure Us May 2019 PDFRonyNo ratings yet
- Overpressure Relief Valve ProsedureDocument3 pagesOverpressure Relief Valve ProsedureKosNo ratings yet
- 2.2 Psychological PerspectiveDocument17 pages2.2 Psychological PerspectiveMaica LagareNo ratings yet
- Q02-Chem - 1023 - Final - ExamDocument5 pagesQ02-Chem - 1023 - Final - ExamRodríguez Rito AméricaNo ratings yet
- Header Specification: Mplab Icd 2Document12 pagesHeader Specification: Mplab Icd 2knoppix2008No ratings yet
- Trans-Amf Eng Man v44Document84 pagesTrans-Amf Eng Man v44AyeminThetNo ratings yet
- Hiponatremia Acute ApendicitisDocument13 pagesHiponatremia Acute ApendicitisDeliciousNo ratings yet
- Series 956: Steyning Way, Bognor Regis, Solartron Metrology, West Sussex, PO22 9ST UKDocument17 pagesSeries 956: Steyning Way, Bognor Regis, Solartron Metrology, West Sussex, PO22 9ST UKAndresNo ratings yet
- Document of Galois Counter ModeDocument16 pagesDocument of Galois Counter Modesantosh chNo ratings yet
- iCE40UltraFamilyDataSheet PDFDocument42 pagesiCE40UltraFamilyDataSheet PDFson_gotenNo ratings yet
- IdeaPad 5 15ALC05 82LN00AKLMDocument2 pagesIdeaPad 5 15ALC05 82LN00AKLMChristian MendozaNo ratings yet
- NC101 Module 1Document6 pagesNC101 Module 1Sarah May Nacion MorescoNo ratings yet
- Is 516 Method of Test For Strength of ConcreteDocument25 pagesIs 516 Method of Test For Strength of Concreteselva_65195078% (9)
- РАЗЛИКИ 200002Document31 pagesРАЗЛИКИ 200002MamattiNo ratings yet
- Stenton Community TurbineDocument13 pagesStenton Community TurbineEttie SpencerNo ratings yet
- Important Filipino ThinkersDocument29 pagesImportant Filipino ThinkersMary Claire Amado100% (1)
- E11 - Unit 10 (Basic) - Test 2Document3 pagesE11 - Unit 10 (Basic) - Test 2Đỗ Cát TiênNo ratings yet
- Cambridge IGCSE: PHYSICS 0625/32Document16 pagesCambridge IGCSE: PHYSICS 0625/32wongwahsengNo ratings yet