Electric Circuit

 It is a closed path, composed of active and

passive elements.
 Active Element : It supplies energy to the
circuit.
 Passive Element : It receives energy and then
1) either converts it to heat,
as in a Resistance (R).
2) or stores it in
(a) Electric Field, as in a Capacitor (C).
(b) Magnetic Field, as in an Inductor (L).
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 1
Energy Sources
 Classification
Independent Source Or Dependent Source
Voltage Source Or Current Source
DC Source Or AC Source
Ideal Source Or Practical Source

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 2
Independent Ideal Voltage
Source
Source
Load

Note that the source determines the voltage, but the

current is determined by the load.
The source has zero internal resistance.
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 3
 The voltage source is said to be idle if the output
terminals are open such that i = 0.
 When turned off (killed or made inactive), so that v =
0, it is equivalent to a short circuit.
 Reference Marks : One terminal is marked plus and the
other minus. (Oversimplification; one mark can be
omitted.)
 When actual polarity is opposite to the reference
marks, the voltage is a negative number.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 4
Independent Ideal Current
Source
Source
Load

Note that the source determines the current, but the

voltage is determined by the load.

The Source has infinite internal resistance (Ri).

Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 5
 The current source is said to be idle if the output
terminals are shorted together, such that v = 0.
 When turned off (killed or made inactive), so that i = 0,
it is equivalent to an open circuit.
 Reference Marks : An arrow is put.
 When actual direction of current is opposite to the
reference (arrow) direction, the current is a negative
number.
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 6
Do you observe duality ?

The roles for the current and voltage are

interchanged in the two sources.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 7
Practical Voltage Source

It is represented by an ideal voltage source in series

with an internal resistance (RSV).

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 8
Practical Current Source

It is modelled as an ideal current source in parallel

with an internal resistance (RSI).

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 9
 Source Transformation
 A practical current source can be converted
into its equivalent practical voltage source,
and vice versa.
 This conversion is valid only for the external
load connected across the terminals of the
source.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 10
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 11
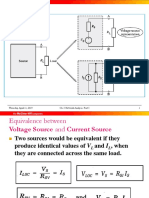
Equivalence between
Voltage Source and Current
Source
 Two sources would be equivalent if they produce
identical values of VL and IL, when they are connected
across the same load.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 12
 Series and Parallel
Combinations
What would be the net emf of the combination
if two ideal voltage sources of 2 V and 4 V are
connected in series so as to aid each other?
Click
 Ans. 6 V
 What would be the net emf of the combination
if two ideal voltage sources of 4 V and 4 V are
connected in parallel ? 4 V or 8 V ? Click
 Ans. Obviously, it should be 4 V

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 13
 What would be the net emf of the combination if two
ideal voltage sources of 2 V and 4 V are connected in
parallel ? 2 V or 4 V or 3 V ? Click
 The question seems to be quite tricky!
Click
 Ans. The question is wrong. The question contradicts
itself.
 Ideal Voltage Sources in parallel are permissible
only when each has the same terminal voltage at
every instant of time.
 What is its dual ?

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 14
Ideal Voltage Sources
Connected in Series

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 15
Ideal Current Sources
Connected in Parallel

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 16
Practical Current Sources
Connected in Series

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 17
 Practical Voltage Sources
Connected in Parallel

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 18
 Example 1 : Reduce the network shown in
figure to its simplest possible form by using
source transformation.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 19
Solution

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 20
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 21
Example 2

 In the given figure,

(a) If RL = 80 Ω, find current iL.
(b) Transform the practical current source into a
practical voltage source and find iL if RL = 80 Ω again.
(c) Find the power drawn from the ideal source in each
case.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 22
Solution :
20
(a) iL  (100)   20 mA
20  80
2
(b) iL   20 mA
80  20
(c) vL  iL  RL  (20 mA)(80 )  1.6 V Click

P  vL  I  (1.6 V )(100 mA)  160 mW Click

Click
In the second case,
P  iL  V  (20 mA)(2 V)  40 mW

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 23
Benchmark Example 3
 Take the benchmark example of the circuit
given in figure. Using source transformation,
determine the voltage v across 3-Ω resistor.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 24
 Solutio
n:
Transforming the 4-A current source into a
voltage source,

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 25
 Combining the two voltage sources,

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 26
Again transforming the voltage source into
current source,

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 27
Combining the two current sources we get Fig.
(e). Transforming this current source into
voltage source (Fig. f )

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 28
 Combining the two resistances, we get Fig.
(g).

Finally, using voltage

divider, we get

3
v  5  2.5 V
33

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 29
Kirchhoff’s Laws
 (1) KCL : Algebraic sum of currents
meeting at a junction of conductors in a
circuit is zero.
 It is simply a restatement of the principle

of conservation of charge.
b

I
j 1
j 0

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 30
 (2) KVL :The algebraic sum of voltages
around a closed circuit or a loop is zero.
 It is simply a restatement of the principle of
conservation of energy.

v
j 1
j 0

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 31
Polarity of Voltages

Note that polarity of the voltage (emf) across a

battery does not depend upon the assumed
direction of current.
Wednesday, May 13, 202
0
Ch. 3 Network Analysis- Part I Next 32
Applying KVL

1. Select a closed loop.

2. Mark the voltage polarity (+ and -) across
each element in the closed loop.
3. Go round the selected loop, and add up
all the voltages with + or – signs.
4. Any one of the following two rules can be
followed :

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 33
(i) Rule 1 : While travelling, if you meet a
voltage rise, write the voltage with positive sign ;
if you meet a voltage drop, write the voltage with
negative sign.
(ii) Rule 2 : While travelling, write the voltage
with positive sign if + is encountered first; write
the voltage with negative sign if – is encountered
first.
We shall be following Rule 1, as it has a strong
analogy with the physical height (altitude) of a
place.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 34
 Example 5 : Use KVL to find vR2 and vx.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 35
For finding vR2, we write KVL eqn. going
around loop abgha clockwise : Click

 36  vR 2  4  0  vR 2  32 V

If you choose to go around the loop

Click
anticlockwise, you get
 4  36  vR 2  0  vR 2  32 V

Giving the same result.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 36
There are two ways to determine vx
1) We can consider this voltage as the voltage
across the gap from d to f. Writing KVL
(habcdfgh) : Click
 4  36  12  14  v x  0
vx  6 V
2) Knowing vR2 , apply a short-cut (bcdfgb) :
Click
 12  14  v x  32  0
vx  6 V

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 37
Important Note about KVL
 The assumed direction of current through a
resistor and the polarity of voltage across it
are always in conformity.
 The end into which the current enters is
marked positive.
 Passive-element sign convention.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 38
Example 6 : Find the current
supplied by the 60-V source in the
network.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 39
Solution :
 We need not find the currents I1, I2 and I3.
 Instead, we reduce the network.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 40
Example 7 : Determine the value of
current I.

2–3–I–4=0 or I = -5 A

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 41
Example 8

Using KCL and KVL, determine the currents ix

and iy in the network shown.

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 42
Solution : Using KCL, the currents in other branches
are marked as shown. Writing KVL equations for the
loops 1, 2 and 3,
100  10 I1  5I x  0
 5 I x  0 I y  10 I1  100
5I x  50  2( I1  I x )  2 I y  0
 7 I x  2 I y  2 I1  50
 2 I y  50  3( I1  I x  I y )  0
 3I x  5 I y  3I1  50

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 43
Writing the above equations in matrix form, Click

5 0 10   I x  100 
7     
 2  2  I y    50 ;
3 5  3  I   50
 1
Using Calculator, we solve for Ix and Iy,
Click
I x  3.87 A; and I y  0.51 A

Wednesday, May 13, 202

0
Ch. 3 Network Analysis- Part I Next 44