Professional Documents
Culture Documents
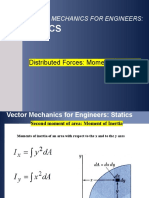
Review Problems Chapter 6
Review Problems Chapter 6
Uploaded by
Yue FeiCopyright:
Available Formats
You might also like
- HW 4 SolutionDocument4 pagesHW 4 Solution万宇恒No ratings yet
- P0807Document5 pagesP0807Adnan KhaldunNo ratings yet
- 01 42 13 - Abbreviations and SymbolsDocument4 pages01 42 13 - Abbreviations and SymbolsshauhramNo ratings yet
- Sample On Operation Management in Business by Instant Essay WritingDocument18 pagesSample On Operation Management in Business by Instant Essay WritingInstant Essay Writing100% (1)
- Finite Element Method (ME G512) Comprehensive Exam: Birla Institute of Technology & Science, Pilani - Hyderabad CampusDocument4 pagesFinite Element Method (ME G512) Comprehensive Exam: Birla Institute of Technology & Science, Pilani - Hyderabad Campustarun saddhahaqNo ratings yet
- Chapter 6: Center of Gravity and CentroidDocument30 pagesChapter 6: Center of Gravity and CentroidJAL4No ratings yet
- Grand Test-1 Key & HintsDocument8 pagesGrand Test-1 Key & HintsM JEEVARATHNAM NAIDUNo ratings yet
- Printed Pages-4 (2×5 10) : (Sem. Ii) Theory Examination 2013-14Document2 pagesPrinted Pages-4 (2×5 10) : (Sem. Ii) Theory Examination 2013-14Mukesh BijalwanNo ratings yet
- Phys 431Document2 pagesPhys 431Yeganeh KhabbazianNo ratings yet
- Physics Advanced Level Problem Solving (ALPS-1) - SolutionDocument16 pagesPhysics Advanced Level Problem Solving (ALPS-1) - SolutionIshan AgnohotriNo ratings yet
- 17339-28-07 Morning Maths 2022Document11 pages17339-28-07 Morning Maths 2022princekumarg013No ratings yet
- Quant Mech Curs 2018 C7-RDocument17 pagesQuant Mech Curs 2018 C7-RsevestreanalinNo ratings yet
- نسخة من Control Tutorial 2Document14 pagesنسخة من Control Tutorial 2eslamelshrwedy2000No ratings yet
- ESC201T L11 RLC CircuitsDocument31 pagesESC201T L11 RLC CircuitsRachit MahajanNo ratings yet
- Y X X Y: Visit Us At: WWW - Nodia.co - inDocument3 pagesY X X Y: Visit Us At: WWW - Nodia.co - inUnique CreationNo ratings yet
- Clase 10 Calculo Numerico IDocument28 pagesClase 10 Calculo Numerico IenriqueNo ratings yet
- 18mab102t TutorialDocument2 pages18mab102t TutorialRohan MohataNo ratings yet
- P0822Document4 pagesP0822Adnan KhaldunNo ratings yet
- Cse I Engineering Mathematics I l3Document23 pagesCse I Engineering Mathematics I l3Venkatesh PawarNo ratings yet
- Assignment 2Document1 pageAssignment 2Usman SarfrazNo ratings yet
- Emir Mentor Paper PDFDocument43 pagesEmir Mentor Paper PDFJagadish KgNo ratings yet
- E F G E G: Visit Us At: WWW - Nodia.co - inDocument3 pagesE F G E G: Visit Us At: WWW - Nodia.co - inUnique CreationNo ratings yet
- Chapter 9 Part 1Document26 pagesChapter 9 Part 1Ahmed AliNo ratings yet
- Lecture 11 - ME 241 - 04 Oct 2015 (Problems)Document24 pagesLecture 11 - ME 241 - 04 Oct 2015 (Problems)kumar7aritra7royNo ratings yet
- Vector Fields and Solutions To Ordinary Differential Equations UsingDocument10 pagesVector Fields and Solutions To Ordinary Differential Equations UsingphysicsnewblolNo ratings yet
- 15 1D Barrier ProblemsDocument23 pages15 1D Barrier ProblemsengshimaaNo ratings yet
- CENTROID (One Dimension) : Engineering Mechanics Cme 1302Document5 pagesCENTROID (One Dimension) : Engineering Mechanics Cme 1302santhiyaperemelNo ratings yet
- Gate 2003 2017 Papers Solved PDFDocument445 pagesGate 2003 2017 Papers Solved PDFraghavNo ratings yet
- Applied Mathematics II (E5)Document2 pagesApplied Mathematics II (E5)eliyasworku2No ratings yet
- Stability of Elastic Structures: Problem 9-1Document18 pagesStability of Elastic Structures: Problem 9-1Aravind BhashyamNo ratings yet
- Chapter 23 Electric Force & Electric Field IIDocument32 pagesChapter 23 Electric Force & Electric Field IIImran ParvezNo ratings yet
- Torsional Vibration Finite Elements: 6.1 Formation of Traditional Inertia MatrixDocument12 pagesTorsional Vibration Finite Elements: 6.1 Formation of Traditional Inertia Matrixابو المعالي الهمامNo ratings yet
- Chapter7 Rev4Document46 pagesChapter7 Rev4PoPoNo ratings yet
- Review For Stress AnalysisDocument15 pagesReview For Stress Analysissuthur27No ratings yet
- Grand Test-4 Key & HintsDocument9 pagesGrand Test-4 Key & HintsM JEEVARATHNAM NAIDUNo ratings yet
- Lecture 1cDocument15 pagesLecture 1cYusuf GulNo ratings yet
- Detailed Solution of GATE-2010 in Electronics&Communication EngineeringDocument14 pagesDetailed Solution of GATE-2010 in Electronics&Communication EngineeringschndNo ratings yet
- 2023 JEE Advanced-3-PAPER-2 - SolutionsDocument13 pages2023 JEE Advanced-3-PAPER-2 - SolutionsAryan SapraNo ratings yet
- Exp-7 PlotDocument4 pagesExp-7 PlotSwaroop MallickNo ratings yet
- A Unified Approach For Designing CapacitDocument6 pagesA Unified Approach For Designing CapacitMehmet AKBABANo ratings yet
- Bill Mosley John Bungey & Ray Hulse: Reinforced Concrete Design To EC2Document33 pagesBill Mosley John Bungey & Ray Hulse: Reinforced Concrete Design To EC2RyanWongJiaHanNo ratings yet
- Application of Quantum in ChemistryDocument37 pagesApplication of Quantum in ChemistryRahul SinghNo ratings yet
- Lecture 3: Methods and Terminology, Part IDocument15 pagesLecture 3: Methods and Terminology, Part IRajkishore DasNo ratings yet
- Fall 06 EEE-241 Open Book/note 1. Find The Unit-Step Response of The Following SystemDocument2 pagesFall 06 EEE-241 Open Book/note 1. Find The Unit-Step Response of The Following SystemAnonymous AFFiZnNo ratings yet
- Sr. Part Test-2 Key and HintsDocument9 pagesSr. Part Test-2 Key and HintsM JEEVARATHNAM NAIDUNo ratings yet
- Time: 3 Hours GATE Full Length Mock Test - F Marks: 100Document12 pagesTime: 3 Hours GATE Full Length Mock Test - F Marks: 100BsauceNo ratings yet
- PDF 5Document17 pagesPDF 5James BundNo ratings yet
- TH Differential Calculus Solution PDFDocument4 pagesTH Differential Calculus Solution PDFEdwin Quinlat DevizaNo ratings yet
- Parabola Npyq1 KeyDocument4 pagesParabola Npyq1 Keybacehor245No ratings yet
- JEE Main 2021 - 22 - DC Circuits - SolutionsDocument19 pagesJEE Main 2021 - 22 - DC Circuits - Solutionscarterjjohn02No ratings yet
- JAM Test Series 4 of Career EndeavourDocument12 pagesJAM Test Series 4 of Career EndeavourSouradip DasNo ratings yet
- Lecture On Truss StructureDocument17 pagesLecture On Truss Structurepreciouspearl99100% (1)
- Sri Chaitanya IIT Academy, India: KEY Sheet PhysicsDocument9 pagesSri Chaitanya IIT Academy, India: KEY Sheet PhysicsPrabhakar BandaruNo ratings yet
- Universidad Nacional Autónoma Altoandina de Tarma: Ep Ingeniería AgroindusttrialDocument1 pageUniversidad Nacional Autónoma Altoandina de Tarma: Ep Ingeniería AgroindusttrialImanol Jesus Palpa ChavezNo ratings yet
- KGH Xs GH KGH CE GH KGH: Mech / Elec Analogy Nyquist Criteria State - SpaceDocument1 pageKGH Xs GH KGH CE GH KGH: Mech / Elec Analogy Nyquist Criteria State - Spacejohn dongNo ratings yet
- Physics Advanced Level Problem Solving (ALPS-7) - SolutionDocument12 pagesPhysics Advanced Level Problem Solving (ALPS-7) - SolutionAnanmay ChauhanNo ratings yet
- 05-02-22 JR - Iit Star Co-Sc (Model-A) Jee Adv 2017 (P-I) Wat-38 Key & SolDocument10 pages05-02-22 JR - Iit Star Co-Sc (Model-A) Jee Adv 2017 (P-I) Wat-38 Key & SolChembzzz ytNo ratings yet
- Math (1st) May2022Document3 pagesMath (1st) May2022kostaaayushiNo ratings yet
- Chapter 5Document10 pagesChapter 5Young BrotherNo ratings yet
- McQuarrie Chapter 3 ProblemsDocument9 pagesMcQuarrie Chapter 3 ProblemsUpakarasamy LourderajNo ratings yet
- Lecture 10 - Particles in 3D Box and Hydrogen AtomDocument28 pagesLecture 10 - Particles in 3D Box and Hydrogen AtomArc ZeroNo ratings yet
- Statics: Vector Mechanics For EngineersDocument39 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Failure Analysis of Pitching Wire For Low Speed Wind Tunnel (LSWT)Document4 pagesFailure Analysis of Pitching Wire For Low Speed Wind Tunnel (LSWT)Yue FeiNo ratings yet
- Determination of The Stability of Retained Austenite in TRIP-aided Bainitic SteelDocument4 pagesDetermination of The Stability of Retained Austenite in TRIP-aided Bainitic SteelYue FeiNo ratings yet
- Chapter III A Equilibrium 2D: Engineering MechanicsDocument85 pagesChapter III A Equilibrium 2D: Engineering MechanicsYue FeiNo ratings yet
- Library C: A. Assert, Abort B. Edom Erange Eilseq CDocument6 pagesLibrary C: A. Assert, Abort B. Edom Erange Eilseq CYue FeiNo ratings yet
- Standar C Librar1Document7 pagesStandar C Librar1Yue FeiNo ratings yet
- Statics: Vector Mechanics For EngineersDocument32 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Statics: Vector Mechanics For EngineersDocument28 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Vector Mechanics For Engineers: Statics: Equilibrium of Rigid BodiesDocument25 pagesVector Mechanics For Engineers: Statics: Equilibrium of Rigid BodiesYue FeiNo ratings yet
- Chapter 2-Hibbeler-Problem Sets, Homeworks: SectionDocument4 pagesChapter 2-Hibbeler-Problem Sets, Homeworks: SectionYue FeiNo ratings yet
- Vectors and Scalars: Engineering MechanicsDocument82 pagesVectors and Scalars: Engineering MechanicsYue FeiNo ratings yet
- Chapter II A Force Systems 2D: Engineering MechanicsDocument117 pagesChapter II A Force Systems 2D: Engineering MechanicsYue Fei100% (1)
- Chapter II B Force Systems 3D: Engineering MechanicsDocument36 pagesChapter II B Force Systems 3D: Engineering MechanicsYue FeiNo ratings yet
- Chapter Two Force VectorsDocument39 pagesChapter Two Force VectorsYue FeiNo ratings yet
- Review Problems Chapter 2Document17 pagesReview Problems Chapter 2Yue FeiNo ratings yet
- Ujian Metode NumerikDocument15 pagesUjian Metode NumerikYue FeiNo ratings yet
- Chapter 1Document12 pagesChapter 1Yue FeiNo ratings yet
- Metode CramerDocument1 pageMetode CramerYue FeiNo ratings yet
- Rs 71 Ball Mill Sizng-1Document4 pagesRs 71 Ball Mill Sizng-1Dilnesa Ejigu100% (1)
- Libusb-Win32-Changelog-1 2 6 0Document4 pagesLibusb-Win32-Changelog-1 2 6 0N WingNo ratings yet
- Peltier Based Eco-Friendly Smart Refrigerator For Rural AreasDocument4 pagesPeltier Based Eco-Friendly Smart Refrigerator For Rural AreassivaneswaranNo ratings yet
- Almig Screw Air CompDocument8 pagesAlmig Screw Air CompMohamed HarbNo ratings yet
- 02 Oliver NenadovicDocument39 pages02 Oliver NenadovicRinu RavikumarNo ratings yet
- Numerical Methods To Liouville EquationnDocument39 pagesNumerical Methods To Liouville EquationnRachel Baltazar VitancolNo ratings yet
- (Frédéric - Boulanger, - Daniel - Krob, - Gérard - Morel) - Complex Systems Design & Management 2014Document360 pages(Frédéric - Boulanger, - Daniel - Krob, - Gérard - Morel) - Complex Systems Design & Management 2014perry.stamatiouNo ratings yet
- Life of Festo Products BrochureDocument7 pagesLife of Festo Products BrochureLeonardo AlexNo ratings yet
- Fundamentals Chapter-6Document4 pagesFundamentals Chapter-6mocosamsnNo ratings yet
- Mohan ResumeDocument4 pagesMohan ResumeRamesh NaiduNo ratings yet
- Standard Operating Procedure: Vehicle FuelingDocument1 pageStandard Operating Procedure: Vehicle FuelingAnees EkNo ratings yet
- TRIPLE FREQUENCY GENERATOR IC For HHO HYDROGEN CELLDocument4 pagesTRIPLE FREQUENCY GENERATOR IC For HHO HYDROGEN CELLTheotech EletronNo ratings yet
- Ceramic CAD/CAM Materials: An Overview of Clinical Uses and ConsiderationsDocument10 pagesCeramic CAD/CAM Materials: An Overview of Clinical Uses and ConsiderationsNajeeb UllahNo ratings yet
- FormulasDocument5 pagesFormulasPremNo ratings yet
- Bio Data Khan 074Document3 pagesBio Data Khan 074Saoud KhanNo ratings yet
- Receiver Noise Figure MeasurementDocument13 pagesReceiver Noise Figure Measurementعلی بنائیNo ratings yet
- Switch Capacitors Circuits Design and SimulationsDocument14 pagesSwitch Capacitors Circuits Design and SimulationsMuhammad YousafNo ratings yet
- Finite Difference MethodDocument14 pagesFinite Difference MethodOMKAR PansareNo ratings yet
- Linde Hydraulics - HPV-02Document0 pagesLinde Hydraulics - HPV-021antonio100% (1)
- AASHTO Huide Specifications For LRFD Seismic Bridge DesignDocument104 pagesAASHTO Huide Specifications For LRFD Seismic Bridge DesignnigelNo ratings yet
- Gypsum Blocks - Definitions, Requirements and Test Methods: British Standard Bs en 12859:2001Document38 pagesGypsum Blocks - Definitions, Requirements and Test Methods: British Standard Bs en 12859:2001AA0809No ratings yet
- Skill Development ProgrammeDocument5 pagesSkill Development ProgrammeKumar RajeshNo ratings yet
- Targeted CompaniesDocument23 pagesTargeted CompaniesAndrewOberoiNo ratings yet
- PDF Manual190+160Document15 pagesPDF Manual190+160torbenNo ratings yet
- Inorganic Chemistry Lab 2Document7 pagesInorganic Chemistry Lab 2apple75% (4)
- Constraint Effect in Fracture - What Is ItDocument10 pagesConstraint Effect in Fracture - What Is ItSoupramanien KathirvelouNo ratings yet
- Single Axis Tracker Sat Control STL36 Solar Tracker DrawingsDocument1 pageSingle Axis Tracker Sat Control STL36 Solar Tracker DrawingsNahuel BritoNo ratings yet
- Using Boss Tone Studio For Me-25Document12 pagesUsing Boss Tone Studio For Me-25felipe herreraNo ratings yet
Review Problems Chapter 6
Review Problems Chapter 6
Uploaded by
Yue FeiOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Review Problems Chapter 6
Review Problems Chapter 6
Uploaded by
Yue FeiCopyright:
Available Formats
EML 3004C
Problem 6-5 (page 256)
Determine the location (x’,y’) of the centroid of the
shaded area.
Solution:
Area of the differential element dA = ydx = (1/x)dx and xc = x, yc= y/2 = 1/(2x)
2
x
1
xcd A dx
x
0.5
xc xc xc 1.08 in
2
1
1 dA dx
x
0.5
2
1 1
dx
yc d A 2x x
0.5
yc yc in yc 0.541in
2
1
1 dA dx
x
0.5
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-1
EML 3004C
Problem 6-20 (page 259)
Determine the distance y’ to the center of
gravity of the volume. The material is
homogeneous.
Solution:
The volume of the differential thin disk element dV = y^2dz = (a^2-z^2)dz and zc = z
a
z dV
z a z d z
2 2
0 3
zc zc zc a
a 8
1 dV
2 2
a z dz
0
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-2
EML 3004C
Problem 6-25 (page 263)
Determine the location (x’,y’) of
the centroid of the area.
Solution:
ycA 1 [ 4 ( 2) ] 4 [ 8 ( 2) ] 7 [ 4 ( 2) ]
yc yc in yc 4in
A 2( 4) ( 2) 8( 2)
xcA 1 [ 8 ( 2) ] 4[ 2( 4) ( 2) ]
xc xc in xc 2.5in
A 2 ( 4) ( 2) 8 ( 2)
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-3
EML 3004C
Problem 6-35 (page 265)
Determine the distance x’ to the center of gravity of
the generator assembly. The weight and the center
of gravity of each of the various components are
indicated below. What are the vertical relations at
blocks A and B needed to support the assembly?
Solution:
W 200 1000 250 W 1450lb
xc W MA 1450xc 200( 1) 1000( 4) 250( 8)
xc 4.276ft
Equilibrium :
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-4
EML 3004C
Problem 6-35 (continued)
xc 4.276ft
Equilibrium :
MA 0 By ( 10) 1450( 4.276) 0 By 620 lb
Fy 0 A y 620 1450 0 A y 830 lb
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-5
EML 3004C
Problem 6-76 (page 289)
Determine the moment of inertia of the
shaded area about the x axis.
Solution:
Area of the differential element (shaded) dA = 2x dy where x = a/b(b^2-y^2)^1/2, hence
dA = 2x dy = 2a/b(b^2-y^2)^1/2 dy
2 2
x 1 x d x
2 2 1 2 x2 1 x4 d x
Ix x d A Ix Ix
4 4
2 2
3
b
Ix
4
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-6
EML 3004C
Problem 6-82 (page 293)
The composite beam consists of a wide-flange
beam and cover plates welded together as
shown. Determine the moment of inertia of
the cross-sectional area with respect to a
horizontal axis passing through the beam’s
centroid.
Solution:
Ixcxc ( 175) ( 200) 160 170 2 275 15 2 15 275 107.5 mm
1 3 1 3 1 3 2 4
12 12 12
8 4
Ixcxc 1.467 10 mm
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-7
EML 3004C
Problem 6-95 (page 295)
Determine the distance y’ to the centroid of
the plate area.
Solution:
Area of the differential element dA = y dx = (1 - 1/4(x^2)) dx and yc = y/2 = 1/2(1-(1/4)x^2)
2
1
1 2
x 1 x d x
1 1 2
yc d A 2 4 4
2
yc yc m yc 0.4m
2
1 dA 1 1 x2 dx
4
2
Namas Chandra Hibbler
Introduction to Mechanical engineering Chapter 2-8
You might also like
- HW 4 SolutionDocument4 pagesHW 4 Solution万宇恒No ratings yet
- P0807Document5 pagesP0807Adnan KhaldunNo ratings yet
- 01 42 13 - Abbreviations and SymbolsDocument4 pages01 42 13 - Abbreviations and SymbolsshauhramNo ratings yet
- Sample On Operation Management in Business by Instant Essay WritingDocument18 pagesSample On Operation Management in Business by Instant Essay WritingInstant Essay Writing100% (1)
- Finite Element Method (ME G512) Comprehensive Exam: Birla Institute of Technology & Science, Pilani - Hyderabad CampusDocument4 pagesFinite Element Method (ME G512) Comprehensive Exam: Birla Institute of Technology & Science, Pilani - Hyderabad Campustarun saddhahaqNo ratings yet
- Chapter 6: Center of Gravity and CentroidDocument30 pagesChapter 6: Center of Gravity and CentroidJAL4No ratings yet
- Grand Test-1 Key & HintsDocument8 pagesGrand Test-1 Key & HintsM JEEVARATHNAM NAIDUNo ratings yet
- Printed Pages-4 (2×5 10) : (Sem. Ii) Theory Examination 2013-14Document2 pagesPrinted Pages-4 (2×5 10) : (Sem. Ii) Theory Examination 2013-14Mukesh BijalwanNo ratings yet
- Phys 431Document2 pagesPhys 431Yeganeh KhabbazianNo ratings yet
- Physics Advanced Level Problem Solving (ALPS-1) - SolutionDocument16 pagesPhysics Advanced Level Problem Solving (ALPS-1) - SolutionIshan AgnohotriNo ratings yet
- 17339-28-07 Morning Maths 2022Document11 pages17339-28-07 Morning Maths 2022princekumarg013No ratings yet
- Quant Mech Curs 2018 C7-RDocument17 pagesQuant Mech Curs 2018 C7-RsevestreanalinNo ratings yet
- نسخة من Control Tutorial 2Document14 pagesنسخة من Control Tutorial 2eslamelshrwedy2000No ratings yet
- ESC201T L11 RLC CircuitsDocument31 pagesESC201T L11 RLC CircuitsRachit MahajanNo ratings yet
- Y X X Y: Visit Us At: WWW - Nodia.co - inDocument3 pagesY X X Y: Visit Us At: WWW - Nodia.co - inUnique CreationNo ratings yet
- Clase 10 Calculo Numerico IDocument28 pagesClase 10 Calculo Numerico IenriqueNo ratings yet
- 18mab102t TutorialDocument2 pages18mab102t TutorialRohan MohataNo ratings yet
- P0822Document4 pagesP0822Adnan KhaldunNo ratings yet
- Cse I Engineering Mathematics I l3Document23 pagesCse I Engineering Mathematics I l3Venkatesh PawarNo ratings yet
- Assignment 2Document1 pageAssignment 2Usman SarfrazNo ratings yet
- Emir Mentor Paper PDFDocument43 pagesEmir Mentor Paper PDFJagadish KgNo ratings yet
- E F G E G: Visit Us At: WWW - Nodia.co - inDocument3 pagesE F G E G: Visit Us At: WWW - Nodia.co - inUnique CreationNo ratings yet
- Chapter 9 Part 1Document26 pagesChapter 9 Part 1Ahmed AliNo ratings yet
- Lecture 11 - ME 241 - 04 Oct 2015 (Problems)Document24 pagesLecture 11 - ME 241 - 04 Oct 2015 (Problems)kumar7aritra7royNo ratings yet
- Vector Fields and Solutions To Ordinary Differential Equations UsingDocument10 pagesVector Fields and Solutions To Ordinary Differential Equations UsingphysicsnewblolNo ratings yet
- 15 1D Barrier ProblemsDocument23 pages15 1D Barrier ProblemsengshimaaNo ratings yet
- CENTROID (One Dimension) : Engineering Mechanics Cme 1302Document5 pagesCENTROID (One Dimension) : Engineering Mechanics Cme 1302santhiyaperemelNo ratings yet
- Gate 2003 2017 Papers Solved PDFDocument445 pagesGate 2003 2017 Papers Solved PDFraghavNo ratings yet
- Applied Mathematics II (E5)Document2 pagesApplied Mathematics II (E5)eliyasworku2No ratings yet
- Stability of Elastic Structures: Problem 9-1Document18 pagesStability of Elastic Structures: Problem 9-1Aravind BhashyamNo ratings yet
- Chapter 23 Electric Force & Electric Field IIDocument32 pagesChapter 23 Electric Force & Electric Field IIImran ParvezNo ratings yet
- Torsional Vibration Finite Elements: 6.1 Formation of Traditional Inertia MatrixDocument12 pagesTorsional Vibration Finite Elements: 6.1 Formation of Traditional Inertia Matrixابو المعالي الهمامNo ratings yet
- Chapter7 Rev4Document46 pagesChapter7 Rev4PoPoNo ratings yet
- Review For Stress AnalysisDocument15 pagesReview For Stress Analysissuthur27No ratings yet
- Grand Test-4 Key & HintsDocument9 pagesGrand Test-4 Key & HintsM JEEVARATHNAM NAIDUNo ratings yet
- Lecture 1cDocument15 pagesLecture 1cYusuf GulNo ratings yet
- Detailed Solution of GATE-2010 in Electronics&Communication EngineeringDocument14 pagesDetailed Solution of GATE-2010 in Electronics&Communication EngineeringschndNo ratings yet
- 2023 JEE Advanced-3-PAPER-2 - SolutionsDocument13 pages2023 JEE Advanced-3-PAPER-2 - SolutionsAryan SapraNo ratings yet
- Exp-7 PlotDocument4 pagesExp-7 PlotSwaroop MallickNo ratings yet
- A Unified Approach For Designing CapacitDocument6 pagesA Unified Approach For Designing CapacitMehmet AKBABANo ratings yet
- Bill Mosley John Bungey & Ray Hulse: Reinforced Concrete Design To EC2Document33 pagesBill Mosley John Bungey & Ray Hulse: Reinforced Concrete Design To EC2RyanWongJiaHanNo ratings yet
- Application of Quantum in ChemistryDocument37 pagesApplication of Quantum in ChemistryRahul SinghNo ratings yet
- Lecture 3: Methods and Terminology, Part IDocument15 pagesLecture 3: Methods and Terminology, Part IRajkishore DasNo ratings yet
- Fall 06 EEE-241 Open Book/note 1. Find The Unit-Step Response of The Following SystemDocument2 pagesFall 06 EEE-241 Open Book/note 1. Find The Unit-Step Response of The Following SystemAnonymous AFFiZnNo ratings yet
- Sr. Part Test-2 Key and HintsDocument9 pagesSr. Part Test-2 Key and HintsM JEEVARATHNAM NAIDUNo ratings yet
- Time: 3 Hours GATE Full Length Mock Test - F Marks: 100Document12 pagesTime: 3 Hours GATE Full Length Mock Test - F Marks: 100BsauceNo ratings yet
- PDF 5Document17 pagesPDF 5James BundNo ratings yet
- TH Differential Calculus Solution PDFDocument4 pagesTH Differential Calculus Solution PDFEdwin Quinlat DevizaNo ratings yet
- Parabola Npyq1 KeyDocument4 pagesParabola Npyq1 Keybacehor245No ratings yet
- JEE Main 2021 - 22 - DC Circuits - SolutionsDocument19 pagesJEE Main 2021 - 22 - DC Circuits - Solutionscarterjjohn02No ratings yet
- JAM Test Series 4 of Career EndeavourDocument12 pagesJAM Test Series 4 of Career EndeavourSouradip DasNo ratings yet
- Lecture On Truss StructureDocument17 pagesLecture On Truss Structurepreciouspearl99100% (1)
- Sri Chaitanya IIT Academy, India: KEY Sheet PhysicsDocument9 pagesSri Chaitanya IIT Academy, India: KEY Sheet PhysicsPrabhakar BandaruNo ratings yet
- Universidad Nacional Autónoma Altoandina de Tarma: Ep Ingeniería AgroindusttrialDocument1 pageUniversidad Nacional Autónoma Altoandina de Tarma: Ep Ingeniería AgroindusttrialImanol Jesus Palpa ChavezNo ratings yet
- KGH Xs GH KGH CE GH KGH: Mech / Elec Analogy Nyquist Criteria State - SpaceDocument1 pageKGH Xs GH KGH CE GH KGH: Mech / Elec Analogy Nyquist Criteria State - Spacejohn dongNo ratings yet
- Physics Advanced Level Problem Solving (ALPS-7) - SolutionDocument12 pagesPhysics Advanced Level Problem Solving (ALPS-7) - SolutionAnanmay ChauhanNo ratings yet
- 05-02-22 JR - Iit Star Co-Sc (Model-A) Jee Adv 2017 (P-I) Wat-38 Key & SolDocument10 pages05-02-22 JR - Iit Star Co-Sc (Model-A) Jee Adv 2017 (P-I) Wat-38 Key & SolChembzzz ytNo ratings yet
- Math (1st) May2022Document3 pagesMath (1st) May2022kostaaayushiNo ratings yet
- Chapter 5Document10 pagesChapter 5Young BrotherNo ratings yet
- McQuarrie Chapter 3 ProblemsDocument9 pagesMcQuarrie Chapter 3 ProblemsUpakarasamy LourderajNo ratings yet
- Lecture 10 - Particles in 3D Box and Hydrogen AtomDocument28 pagesLecture 10 - Particles in 3D Box and Hydrogen AtomArc ZeroNo ratings yet
- Statics: Vector Mechanics For EngineersDocument39 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Failure Analysis of Pitching Wire For Low Speed Wind Tunnel (LSWT)Document4 pagesFailure Analysis of Pitching Wire For Low Speed Wind Tunnel (LSWT)Yue FeiNo ratings yet
- Determination of The Stability of Retained Austenite in TRIP-aided Bainitic SteelDocument4 pagesDetermination of The Stability of Retained Austenite in TRIP-aided Bainitic SteelYue FeiNo ratings yet
- Chapter III A Equilibrium 2D: Engineering MechanicsDocument85 pagesChapter III A Equilibrium 2D: Engineering MechanicsYue FeiNo ratings yet
- Library C: A. Assert, Abort B. Edom Erange Eilseq CDocument6 pagesLibrary C: A. Assert, Abort B. Edom Erange Eilseq CYue FeiNo ratings yet
- Standar C Librar1Document7 pagesStandar C Librar1Yue FeiNo ratings yet
- Statics: Vector Mechanics For EngineersDocument32 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Statics: Vector Mechanics For EngineersDocument28 pagesStatics: Vector Mechanics For EngineersYue FeiNo ratings yet
- Vector Mechanics For Engineers: Statics: Equilibrium of Rigid BodiesDocument25 pagesVector Mechanics For Engineers: Statics: Equilibrium of Rigid BodiesYue FeiNo ratings yet
- Chapter 2-Hibbeler-Problem Sets, Homeworks: SectionDocument4 pagesChapter 2-Hibbeler-Problem Sets, Homeworks: SectionYue FeiNo ratings yet
- Vectors and Scalars: Engineering MechanicsDocument82 pagesVectors and Scalars: Engineering MechanicsYue FeiNo ratings yet
- Chapter II A Force Systems 2D: Engineering MechanicsDocument117 pagesChapter II A Force Systems 2D: Engineering MechanicsYue Fei100% (1)
- Chapter II B Force Systems 3D: Engineering MechanicsDocument36 pagesChapter II B Force Systems 3D: Engineering MechanicsYue FeiNo ratings yet
- Chapter Two Force VectorsDocument39 pagesChapter Two Force VectorsYue FeiNo ratings yet
- Review Problems Chapter 2Document17 pagesReview Problems Chapter 2Yue FeiNo ratings yet
- Ujian Metode NumerikDocument15 pagesUjian Metode NumerikYue FeiNo ratings yet
- Chapter 1Document12 pagesChapter 1Yue FeiNo ratings yet
- Metode CramerDocument1 pageMetode CramerYue FeiNo ratings yet
- Rs 71 Ball Mill Sizng-1Document4 pagesRs 71 Ball Mill Sizng-1Dilnesa Ejigu100% (1)
- Libusb-Win32-Changelog-1 2 6 0Document4 pagesLibusb-Win32-Changelog-1 2 6 0N WingNo ratings yet
- Peltier Based Eco-Friendly Smart Refrigerator For Rural AreasDocument4 pagesPeltier Based Eco-Friendly Smart Refrigerator For Rural AreassivaneswaranNo ratings yet
- Almig Screw Air CompDocument8 pagesAlmig Screw Air CompMohamed HarbNo ratings yet
- 02 Oliver NenadovicDocument39 pages02 Oliver NenadovicRinu RavikumarNo ratings yet
- Numerical Methods To Liouville EquationnDocument39 pagesNumerical Methods To Liouville EquationnRachel Baltazar VitancolNo ratings yet
- (Frédéric - Boulanger, - Daniel - Krob, - Gérard - Morel) - Complex Systems Design & Management 2014Document360 pages(Frédéric - Boulanger, - Daniel - Krob, - Gérard - Morel) - Complex Systems Design & Management 2014perry.stamatiouNo ratings yet
- Life of Festo Products BrochureDocument7 pagesLife of Festo Products BrochureLeonardo AlexNo ratings yet
- Fundamentals Chapter-6Document4 pagesFundamentals Chapter-6mocosamsnNo ratings yet
- Mohan ResumeDocument4 pagesMohan ResumeRamesh NaiduNo ratings yet
- Standard Operating Procedure: Vehicle FuelingDocument1 pageStandard Operating Procedure: Vehicle FuelingAnees EkNo ratings yet
- TRIPLE FREQUENCY GENERATOR IC For HHO HYDROGEN CELLDocument4 pagesTRIPLE FREQUENCY GENERATOR IC For HHO HYDROGEN CELLTheotech EletronNo ratings yet
- Ceramic CAD/CAM Materials: An Overview of Clinical Uses and ConsiderationsDocument10 pagesCeramic CAD/CAM Materials: An Overview of Clinical Uses and ConsiderationsNajeeb UllahNo ratings yet
- FormulasDocument5 pagesFormulasPremNo ratings yet
- Bio Data Khan 074Document3 pagesBio Data Khan 074Saoud KhanNo ratings yet
- Receiver Noise Figure MeasurementDocument13 pagesReceiver Noise Figure Measurementعلی بنائیNo ratings yet
- Switch Capacitors Circuits Design and SimulationsDocument14 pagesSwitch Capacitors Circuits Design and SimulationsMuhammad YousafNo ratings yet
- Finite Difference MethodDocument14 pagesFinite Difference MethodOMKAR PansareNo ratings yet
- Linde Hydraulics - HPV-02Document0 pagesLinde Hydraulics - HPV-021antonio100% (1)
- AASHTO Huide Specifications For LRFD Seismic Bridge DesignDocument104 pagesAASHTO Huide Specifications For LRFD Seismic Bridge DesignnigelNo ratings yet
- Gypsum Blocks - Definitions, Requirements and Test Methods: British Standard Bs en 12859:2001Document38 pagesGypsum Blocks - Definitions, Requirements and Test Methods: British Standard Bs en 12859:2001AA0809No ratings yet
- Skill Development ProgrammeDocument5 pagesSkill Development ProgrammeKumar RajeshNo ratings yet
- Targeted CompaniesDocument23 pagesTargeted CompaniesAndrewOberoiNo ratings yet
- PDF Manual190+160Document15 pagesPDF Manual190+160torbenNo ratings yet
- Inorganic Chemistry Lab 2Document7 pagesInorganic Chemistry Lab 2apple75% (4)
- Constraint Effect in Fracture - What Is ItDocument10 pagesConstraint Effect in Fracture - What Is ItSoupramanien KathirvelouNo ratings yet
- Single Axis Tracker Sat Control STL36 Solar Tracker DrawingsDocument1 pageSingle Axis Tracker Sat Control STL36 Solar Tracker DrawingsNahuel BritoNo ratings yet
- Using Boss Tone Studio For Me-25Document12 pagesUsing Boss Tone Studio For Me-25felipe herreraNo ratings yet