Chapter 6: Probability

Probability

• Probability is a method for measuring and

quantifying the likelihood of obtaining a specific
sample from a specific population.
• We define probability as a fraction or a
proportion.
• The probability of any specific outcome is
determined by a ratio comparing the frequency
of occurrence for that outcome relative to the
total number of possible outcomes.
 Probability (cont'd.)

• Whenever the scores in a population are variable, it

is impossible to predict with perfect accuracy exactly
which score(s) will be obtained when you take a
sample from the population.
– In this situation, researchers rely on probability to
determine the relative likelihood for specific samples.
– Thus, although you may not be able to predict exactly
which value(s) will be obtained for a sample, it is
possible to determine which outcomes have high
probability and which have low probability.
 Probability and Sampling
• To assure that the definition of probability is
accurate, the use of random sampling is
necessary.
– Random sampling requires that each member of
a population has an equal chance of being
selected.
– Independent random sampling includes the
conditions of random sampling and further
requires that the probability of being selected
remains constant for each selection
 Probability (cont'd.)

• When a population of scores is represented by a

frequency distribution, probabilities can be
defined by proportions of the distribution.
• Probability values are expressed by a fraction or
proportion.
• In graphs, probability can be defined as a
proportion of area under the curve.
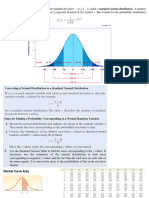
Probability and the Normal Distribution
Probability and the Normal Distribution

• If a vertical line is drawn through a normal

distribution, several things occur.
– The line divides the distribution into two sections.
The larger section is called the body and the
smaller section is called the tail.
– The exact location of the line can be specified by
a z-score.
 Probability and the Normal
Distribution (cont'd.)
• The unit normal table lists several different
proportions corresponding to each z-score
location.
– Column A of the table lists z-score values.
– For each z-score location, columns B and C list the
proportions in the body and tail, respectively.
– Finally, column D lists the proportion between the
mean and the z-score location.
• Because probability is equivalent to proportion,
the table values can also be used to determine
probabilities.
Probability and the Normal Distribution
(cont'd.)
• To find the probability corresponding to a
particular score (X value), you first transform the
score into a z-score, then look up the z-score in
the table and read across the row to find the
appropriate proportion/probability.
• To find the score (X value) corresponding to a
particular proportion, you first look up the
proportion in the table, read across the row to
find the corresponding z-score, and then
transform the z-score into an X value.
Probability and the Normal Distribution
(cont'd.)
• The normal distribution is symmetrical; therefore,
the proportions will be the same for the positive
and negative values of a specific z-score.
• Proportions are always positive, even if the
corresponding z-score is negative.
• A negative z-score means that the tail of the
distribution is on the left side and the body is on
the right, and vice versa for a positive z-score.
Probability and the Normal Distribution
(cont'd.)
 Percentiles and Percentile Ranks

• The percentile rank for a specific X value is the

percentage of individuals with scores at or below
that value.
• When a score is referred to by its rank, the score
is called a percentile. The percentile rank for a
score in a normal distribution is simply the
proportion to the left of the score.
 Probability and the Binomial
Distribution
• Binomial distributions are formed by a series of
observations (for example, 100 coin tosses) for
which there are exactly two possible outcomes
(heads and tails)
• The two outcomes are identified as A and B, with
probabilities of p(A) = p and p(B) = q.
• p + q = 1.00
• The distribution shows the probability for each
value of X, where X is the number of occurrences
of A in a series of n observations.
 Probability and the Binomial
Distribution (cont'd.)
• When pn and qn are both greater than 10, the
binomial distribution is closely approximated by
a normal distribution with a mean of μ = pn and
a standard deviation of σ = npq.
• In this situation, a z-score can be computed for
each value of X and the unit normal table can be
used to determine probabilities for specific
outcomes.
 Probability and Inferential Statistics

• Probability is important because it establishes a

link between samples and populations.
• For any known population, it is possible to
determine the probability of obtaining any
specific sample.
• In later chapters, we will use this link as the
foundation for inferential statistics.
 Probability and Inferential Statistics
(cont'd.)
• The general goal of inferential statistics is to use
the information from a sample to reach a general
conclusion (inference) about an unknown
population.
• Typically a researcher begins with a sample.
 Probability and Inferential Statistics
(cont'd.)
• If the sample has a high probability of being
obtained from a specific population, then the
researcher can conclude that the sample is likely
to have come from that population.
• If the sample has a very low probability of being
obtained from a specific population, then it is
reasonable for the researcher to conclude that
the specific population is probably not the
source for the sample.